|
|
Post by the light works on Feb 2, 2022 16:44:22 GMT
as geeks are wont to do I was mulling over the physics of FTL travel, and started wondering, with particles increasing in mass as they are accelerated close to light speed, what would that have on the thrust from a rocket engine if the rocket exhaust was accelerated significantly close to the speed of light. would it correspond to the stationary mass of the exhaust or would it correspond to the adjusted mass?
|
|
|
|
Post by GTCGreg on Feb 2, 2022 19:04:20 GMT
My guess (and that's all it is) would be adjusted mass. I would think the rocket would accelerate pretty fast at first. But as the rocket started to get closer to light speed, its mass would also increase thus slowing down its acceleration. I think this is one of those so close but so far problems.
|
|
|
|
Post by the light works on Feb 2, 2022 19:10:28 GMT
My guess (and that's all it is) would be adjusted mass. I would think the rocket would accelerate pretty fast at first. But as the rocket started to get closer to light speed, its mass would also increase thus slowing down its acceleration. I think this is one of those so close but so far problems. I was wondering because it seems it might be bordering on over unity, but I guess since it takes a phenomenal amount of energy to accelerate your exhaust gases to that velocity, maybe it isn't. I was curious about the difference between fuel load and reaction mass, for the most part. |
|
|
|
Post by GTCGreg on Feb 2, 2022 19:57:58 GMT
And there's the problem. Not too bad until you hit about 90% Speed of Light. Then things start to go off the rail. 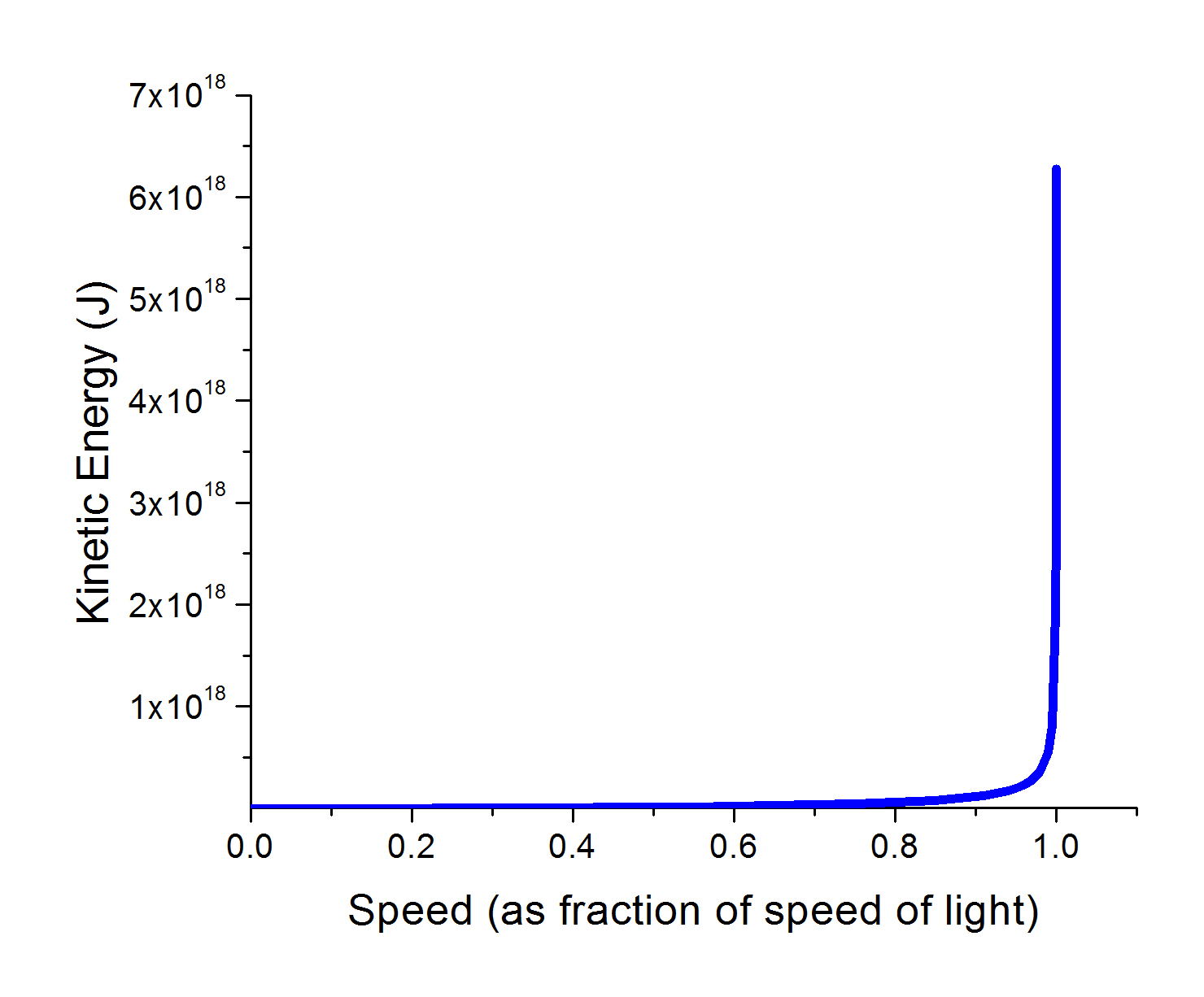 |
|
|
|
Post by wvengineer on Feb 4, 2022 13:47:52 GMT
Another issue is the energy imparted by the reaction mass is relative to the speed of the two. If you have a very high velocity rocket mass from the rocket and a slow moving ship, then the rocket will impart a lot of energy and you'll get a large change in velocity (delta V). However, the faster the rocket is going, the less Delta V you will get from the same rocket engine. You will get to a point where the rocket just isn't able push the ship any faster. Basically the ability of the rocket to speed up the ship would look like GTC's chart flipped up side down. As your ship gets closer to the energy of your rocket exhaust, the delta V gets less and less until the two are equal and your Delta V is 0.
Note, I'm ignoring the use of fuel and changing mass of the ship. That just make the math more complicated.
|
|
|
|
Post by the light works on Feb 4, 2022 15:11:11 GMT
Another issue is the energy imparted by the reaction mass is relative to the speed of the two. If you have a very high velocity rocket mass from the rocket and a slow moving ship, then the rocket will impart a lot of energy and you'll get a large change in velocity (delta V). However, the faster the rocket is going, the less Delta V you will get from the same rocket engine. You will get to a point where the rocket just isn't able push the ship any faster. Basically the ability of the rocket to speed up the ship would look like GTC's chart flipped up side down. As your ship gets closer to the energy of your rocket exhaust, the delta V gets less and less until the two are equal and your Delta V is 0. Note, I'm ignoring the use of fuel and changing mass of the ship. That just make the math more complicated. yeah, there's a reason most science fiction writers don't go into propulsion mechanics. much easier to just go to warp. but maybe that's how TIE fighters get so much acceleration out of ion engines. maybe the engines are in series instead of parallel, so they accelerate the ions to a higher exhaust velocity, giving them better acceleration at the slow speeds Star Wars ships in sublight travel at. |
|
|
|
Post by rmc on Feb 5, 2022 13:18:21 GMT
as geeks are wont to do I was mulling over the physics of FTL travel, and started wondering, with particles increasing in mass as they are accelerated close to light speed, what would that have on the thrust from a rocket engine if the rocket exhaust was accelerated significantly close to the speed of light. would it correspond to the stationary mass of the exhaust or would it correspond to the adjusted mass? There is gravitational mass and there is inertial mass. For these considerations we are looking only at inertial mass... the amount of resistance to changes in velocity... and, MOST IMPORTANTLY, those changes are seen by OUTSIDE observers to such systems. To account for light (causality) and its constant nature: Gravitational mass is a way of defining how much stuff there is in an object. During acceleration, the stuff remains the SAME amount, but energy content goes up, thereby INERTIAL mass goes up meaning the resistance to changes in velocity are greater and greater... as accounted by an outside observer. So, as an object, its fuel, its exhaust all approach the velocity of electromagnetism (C), within its specific locale NOTHING changes: it has the same weight and mass as before moving, it sees light going the speed of light within its location. So objects aboard the vessel see nothing different. (This INCLUDES the exhaust and the WAY exhaust behaves locally). If you've turned on headlights and crawled out to check, they'd be glowing away, speed of light zipping ahead of you at EXACTLY "C" the speed of light. If you went round to the tailpipe, exhaust looks like it always did, whatever it did. The all important adjustment here, mathematically, is "gamma FACTOR". And the adjustments are done to the kinetic energy equation to account for relativistic differences. All the relativistic differences are, are those caused when the speed of light stays the same for every moving or non-moving reference point in space: the constant speed of light. Gamma is a geometric analysis of this constant speed of light phenomena. It is plainly visible when visualizing the type of photon clock Einstein describes. Between two parallel mirrors 30 cm apart, as a photon bounces between them it forms a straight line for the viewer next to the clock, (straight line up and down) but as this viewer-clock system passes an outside observer, the observer sees a photon tracing an angled longer path. The angle isn't as important as the position of the photon in each system. Or, more accurately, the angle is JUST as important as positions in each... Outside, for the observer, the photon is part way to the mirror along said angled path because the photon goes the speed C along this LONGER path. Meanwhile, for the viewer inside, the photon is at the surface of the mirror during this same instant along a shorter path. And all of the differences are due to the fact that light cannot change its speed for the various viewers and observers. Had light been faster for the outside observer, it would have passed along its longer, angled path faster and met the mirror at the same time that the onboard viewer sees this happen. BUT, light cannot adjust its speed, and for the observer the path is LONGER. So each person sees something different with regard to the photon clock and the position of the bouncing photon. Trigonometry (right triangle formula x^2 + y^2 = r^2) is used upon this model of the photon clock (the positions of the photons) and we are given the transformation, gamma factor. This factor is used upon lengths, times, masses for relativistic problems. Kinetic energy is half of mass times its velocity squared. The mass in this fundamental equation is INERTIAL mass, NOT stuff-mass (Gravitational Mass) Ke=m(V squared)/2 Since we start with kinetic energy formula, when it's adjusted using the gamma factor, it becomes E=m(C squared). We observers give systems more energy content than they'd normally have in order to account for OUR outside observations, using the gamma factor. (Length, time, inertial mass) That's the discussion where "increasing" so called mass came from. Pay it no mind, unless you are interested in "energy content" If so, look into the Hamiltonian. Here is a demonstration of using gamma factor to make adjustments: Note that gamma is usually a factor basically close to one, such that nothing changes when you multiply by one. But, increase the velocity and that factor slowly becomes just greater than one. Like 1.00001 and so on. Fun fact: Massless items move through space at C, and time not at all. Meanwhile, at rest items with mass (inertial or otherwise) travel through time at C and through space less than C. Once the motion through space increases, its "motion" through time decreases accordingly. |
|
|
|
Post by GTCGreg on Feb 5, 2022 14:50:22 GMT
Very interesting and well explained.
So today I've learned something new.
Thank you!
|
|
|
|
Post by the light works on Feb 5, 2022 16:43:48 GMT
as geeks are wont to do I was mulling over the physics of FTL travel, and started wondering, with particles increasing in mass as they are accelerated close to light speed, what would that have on the thrust from a rocket engine if the rocket exhaust was accelerated significantly close to the speed of light. would it correspond to the stationary mass of the exhaust or would it correspond to the adjusted mass? There is gravitational mass and there is inertial mass. For these considerations we are looking only at inertial mass... the amount of resistance to changes in velocity... and, MOST IMPORTANTLY, those changes are seen by OUTSIDE observers to such systems. To account for light (causality) and its constant nature: Gravitational mass is a way of defining how much stuff there is in an object. During acceleration, the stuff remains the SAME amount, but energy content goes up, thereby INERTIAL mass goes up meaning the resistance to changes in velocity are greater and greater... as accounted by an outside observer. So, as an object, its fuel, its exhaust all approach the velocity of electromagnetism (C), within its specific locale NOTHING changes: it has the same weight and mass as before moving, it sees light going the speed of light within its location. So objects aboard the vessel see nothing different. (This INCLUDES the exhaust and the WAY exhaust behaves locally). If you've turned on headlights and crawled out to check, they'd be glowing away, speed of light zipping ahead of you at EXACTLY "C" the speed of light. If you went round to the tailpipe, exhaust looks like it always did, whatever it did. The all important adjustment here, mathematically, is "gamma FACTOR". And the adjustments are done to the kinetic energy equation to account for relativistic differences. All the relativistic differences are, are those caused when the speed of light stays the same for every moving or non-moving reference point in space: the constant speed of light. Gamma is a geometric analysis of this constant speed of light phenomena. It is plainly visible when visualizing the type of photon clock Einstein describes. Between two parallel mirrors 30 cm apart, as a photon bounces between them it forms a straight line for the viewer next to the clock, (straight line up and down) but as this viewer-clock system passes an outside observer, the observer sees a photon tracing an angled longer path. The angle isn't as important as the position of the photon in each system. Or, more accurately, the angle is JUST as important as positions in each... Outside, for the observer, the photon is part way to the mirror along said angled path because the photon goes the speed C along this LONGER path. Meanwhile, for the viewer inside, the photon is at the surface of the mirror during this same instant along a shorter path. And all of the differences are due to the fact that light cannot change its speed for the various viewers and observers. Had light been faster for the outside observer, it would have passed along its longer, angled path faster and met the mirror at the same time that the onboard viewer sees this happen. BUT, light cannot adjust its speed, and for the observer the path is LONGER. So each person sees something different with regard to the photon clock and the position of the bouncing photon. Trigonometry (right triangle formula x^2 + y^2 = r^2) is used upon this model of the photon clock (the positions of the photons) and we are given the transformation, gamma factor. This factor is used upon lengths, times, masses for relativistic problems. Kinetic energy is half of mass times its velocity squared. The mass in this fundamental equation is INERTIAL mass, NOT stuff-mass (Gravitational Mass) Ke=m(V squared)/2 Since we start with kinetic energy formula, when it's adjusted using the gamma factor, it becomes E=m(C squared). We observers give systems more energy content than they'd normally have in order to account for OUR outside observations, using the gamma factor. (Length, time, inertial mass) That's the discussion where "increasing" so called mass came from. Pay it no mind, unless you are interested in "energy content" If so, look into the Hamiltonian. Here is a demonstration of using gamma factor to make adjustments: Note that gamma is usually a factor basically close to one, such that nothing changes when you multiply by one. But, increase the velocity and that factor slowly becomes just greater than one. Like 1.00001 and so on. Fun fact: Massless items move through space at C, and time not at all. Meanwhile, at rest items with mass (inertial or otherwise) travel through time at C and through space less than C. Once the motion through space increases, its "motion" through time decreases accordingly. my primary curiosity is if you take a given mass and project it at a velocity that causes the mass to increase due to coming close to the speed of light, will it impart more reaction than would be accounted for by the velocity? or practically, if your spaceship is carrying a given gravitational mass of fuel, could it improve its fuel efficiency with a thruster design that accelerated the exhaust to velocities that caused an increase in inertial mass? |
|
|
|
Post by rmc on Feb 5, 2022 17:06:25 GMT
As I say, locally, no.
For those zipping along with the spacecraft all masses are as they were. Such that action-reaction between stored propellant and spent fuel is the SAME delta V as before relatively became apparent.
To a so called "stationary" observer on the outside somewhere, he'd note that all kinetic energy values are up significantly though.
|
|
|
|
Post by rmc on Feb 5, 2022 20:19:46 GMT
In the pretty likely chance that my over simplification of the problem includes an answer or answers containing errors of some sort, I'll include this main video that discusses gamma and it's implications, which also references subordinate videos that give a complete background.
|
|
|
|
Post by the light works on Feb 5, 2022 21:05:03 GMT
As I say, locally, no. For those zipping along with the spacecraft all masses are as they were. Such that action-reaction between stored propellant and spent fuel is the SAME delta V as before relatively became apparent. To a so called "stationary" observer on the outside somewhere, he'd note that all kinetic energy values are up significantly though. well, back to the dilithium mines, I guess... |
|
|
|
Post by rmc on Feb 6, 2022 9:56:12 GMT
As I say, locally, no. For those zipping along with the spacecraft all masses are as they were. Such that action-reaction between stored propellant and spent fuel is the SAME delta V as before relatively became apparent. To a so called "stationary" observer on the outside somewhere, he'd note that all kinetic energy values are up significantly though. well, back to the dilithium mines, I guess... Ion drive (from the start) has thrust some fairly small percentage of C. The thrust could stay the same for ion drive the whole trip, unlike liquid propellant. As liquid leaves the craft as spent fuel, mass goes down and thrust goes up unless throttling down. As vessel speed increases toward C, there could be some point in the journey where spent ions basically come to rest in space, immediately after being exhausted out the back of the drive- that point where forward ship velocity has reached beyond expelling velocity of the ion propellants. So, to an observer outside the ion ship, ion propellants would lose whatever relativistic properties they had, if any, as the journey carries on. But, should the ship become fast enough with a constant acceleration, there also becomes a point where expelled propellants (ions) aren't expelled as fast or faster than the ship anymore. At this point, spent propellants, instead of finding themselves stationary, would drift in the same direction as the traveling craft. ... If ion exhaust is 50 km per second, the high end of the usual, than that's only a paltry 0.00016678 C... 0.017 percent the speed of light. So, yeah. Accelerating for a long enough time and your craft will be well beyond that speed. |
|
|
|
Post by the light works on Feb 6, 2022 15:48:25 GMT
well, back to the dilithium mines, I guess... Ion drive (from the start) has thrust some fairly small percentage of C. The thrust could stay the same for ion drive the whole trip, unlike liquid propellant. As liquid leaves the craft as spent fuel, mass goes down and thrust goes up unless throttling down. As vessel speed increases toward C, there could be some point in the journey where spent ions basically come to rest in space, immediately after being exhausted out the back of the drive- that point where forward ship velocity has reached beyond expelling velocity of the ion propellants. So, to an observer outside the ion ship, ion propellants would lose whatever relativistic properties they had, if any, as the journey carries on. But, should the ship become fast enough with a constant acceleration, there also becomes a point where expelled propellants (ions) aren't expelled as fast or faster than the ship anymore. At this point, spent propellants, instead of finding themselves stationary, would drift in the same direction as the traveling craft. ... If ion exhaust is 50 km per second, the high end of the usual, than that's only a paltry 0.00016678 C... 0.017 percent the speed of light. So, yeah. Accelerating for a long enough time and your craft will be well beyond that speed. well, that goes for any form of reaction drive. from walking to scramjet. your theoretical top speed can never exceed how fast you can move your drive components. (relative speed, of course. moving mediums add to your total speed) |
|
|
|
Post by rmc on Feb 6, 2022 16:05:13 GMT
Scramjet must overcome drag.
In basically frictionless environments the exhaust ends up ultimately slower than the vehicle speed ... if you are able to continuously accelerate for long enough.
|
|
|
|
Post by the light works on Feb 6, 2022 16:09:56 GMT
Scramjet must overcome drag. In basically frictionless environments the exhaust ends up ultimately slower than the vehicle speed ... if you are able to continuously accelerate for long enough. everything outside of a classroom must overcome drag. in a classroom environment, a rocket would accelerate until the exhaust could no longer produce a high pressure environment at the nozzle. I'm not good enough at physics to know whether that would exceed the peak velocity of the exhaust or not, but there comes a point where the rocket goes from producing thrust to reducing drag. |
|
|
|
Post by GTCGreg on Feb 6, 2022 19:36:04 GMT
Not a whole lot of drag in the vacuum of space. That’s why the voyager probes are still going.
|
|
|
|
Post by the light works on Feb 6, 2022 21:15:18 GMT
Not a whole lot of drag in the vacuum of space. That’s why the voyager probes are still going. at least as far as we know... have they called home, lately? |
|
|
|
Post by GTCGreg on Feb 7, 2022 1:07:10 GMT
Not a whole lot of drag in the vacuum of space. That’s why the voyager probes are still going. at least as far as we know... have they called home, lately? As of October 2020 they have re-established communications with Voyager 2. The radio telescope that NASA uses to communicate with Voyager has been down for some time for upgrades so they hadn't been able to communicate with the probes. On October 29, 2020 the repairs were completed and two-way communications has resumed. Both Voyager probes were designed for a 5 year life span. It's been 45 years and both probes are still working and in communication with NASA. BTW, it takes 21 hours for a signal from Earth to reach Voyager. That makes it 21 light hours away. |
|
|
|
Post by rmc on Feb 7, 2022 13:13:55 GMT
21 light hours. 24 hours 365.25 days ------------- * ---------------- = 1 day.......... 1 year. 8766 hours ----------- 1 year About 6 trillion miles traveled in a year for a light-year. Light-year = 5.88 trillion miles. 8766 light-hours = 5.88 trillion miles. 21 as a decimal portion of 8766. 21..... n ------ = -- 8766 1 21 = 8766n 21 ------ = n 8766 0.002395619439 = n 21 light hours is 0.002395619439 light-year. So multiply 0.002395619439 with 5.88 trillion miles, and you can get the number of miles traveled thus far. (0.002395619439) * 5,880,000,000,000 miles. 14,086,242,301.3 miles. The number of hours real time is the number of years since it launched and left orbit, those years multiplied by the number of hours in a year (24 * 365.25) or 8766 hours in a year. Let's see, it left orbit during 1977. So, these figures will get vague because Voyager did speed adjustments using the planets and all I'm doing is averaging from earth to where it is now all as one speed, just using 2022-1977 as the number of years. 45 years is 45*8766 hours. 394,470 hours. *** But, it has actually been more like 44.5 years. 44.5 * 8766 = 390,087 hours. Now we can get an average(ish) miles per hour: 14,086,242,301.3 miles ----------------------- 390,087 hours 36,110.5145808 miles/hour. And, the real speed listed by NASA is 38,210 mph. Assuming we trust NASA's information about it's current speed, my guess-estimate, calculating its approximate distance and using some rough approximation of the time traveled, was 2,100 mph slower than what it is in reality. So, I don't see evidence of much in the way of drag. Looks like my distance is 400 million miles short somehow. I calculated 14 billion miles when it's actually 14.4 billion miles away at this point. voyager.jpl.nasa.gov/mission/status/ |
|